Autoencoder

Autoencoder의 4가지 주요 키워드
Unsupervised learning - 학습방법
ML density estimation - MLE
Manifold learning - 차원축소
Generative model learning - 디코더는 생성모델
Autoencoder
레이블이 지정되지 않은 데이터의 효율적인 코딩을 학습하는데 사용되는 인공신경망의 한 종류 (unsupervised learning)
크게 Encoder, Decoder 두 부분으로 나뉘고, Encoder에 들어온 Input 값을 Decoder의 출력인 Output과 동일한 네트워크를 만드는 것이 목적이다. (= 입출력이 동일한 네트워크; L(x, x')를 최소화)
Encoder
Input 값으로 차원이 축소된 Bottleneck hidden layer(=latent space vector; 위 그림에선 z)를 형성한다. (위 그림에선 z)
Decoder
Bottleneck hidden layer로부터 Output 값을 생성해 낸다. (생성모델)
수식 및 학습방법
주어진 변수 및 함수
input = x, output(=reconstructed input) = x'; x, x' ∈ ℝ^d (x와 x'은 동일 차원)
encoder function = g(x): z = g(x) ; z ∈ ℝ^d_z (z의 차원 < x, x'의 차원)
decoder function = f(z): x' = f(z) = f(g(x))
L = ∑L(x, x')
- input data(=x)를 Encoder에 넣어 압축된 벡터 z 값을 얻어낸다.
- 압축된 z 벡터로부터 input data와 같은 차원의 output data(=x') 값을 생성한다.
- 이때, input data와 output data의 차이를 계산한다. (=Loss)
- 해당 Loss 값의 차이를 줄이는 방식으로 z layer를 조정하는 방향으로 학습한다. (argminL(ɸ, θ))
- Loss 함수로는 L1 loss, L2 loss(=MSE), BCE 등이 사용된다.
차원을 왜 축소하는가?
차원의 저주: 데이터의 차원이 증가할 수록 해당 공간의 크기는 기하 급수적으로 증가하게 되고 동일한 개수의 데이터가 있을 때 매우 sparse 한 데이터 분포를 가지게 될 것이다. 데이터의 분포가 sparse 학습이 under fitting 되어 원하는 결과를 얻기 어려워 진다. Dense 한 데이터 분포를 위해 차원을 줄여 동일한 샘플 데이터로 학습이 잘 이루어지도록 해야 한다. 그렇다고 차원을 심하게 줄이면 Over fitting 이 이루어 질 수 있으므로 적당히 해야 한다.
Manifold learning
Manifold 가정: 고차원의 데이터의 밀도는 낮지만, 이들의 집합을 포함하는 저차원의 매니폴드가 있다. 이 저차원의 매니폴드를 벗어나는 순간 밀도는 급격히 낮아진다. → 고차원의 manifold 를 저차원으로 만들어 특징을 쉽게 파악하자.
차원을 줄이게 되면 얻는 가정은 다음과 같다.
의미적으로 가깝다고 생각되는 고차원 공간에서의 두 샘플들 간의 거리가 저차원에서는 먼 경우가 많다.
고차원 공간에서 가까운 두 샘플은 의미적으로는 굉장히 다를 수 있다.
차원의 저주는 고차원에서의 유의미한 거리 측정 방식을 찾기 어렵게 한다.

위 이미지에서 왼쪽 이미지를 고차원, 오른쪽 이미지를 저차원이라 할 때,
고차원에서 B는 A1이 A2보다 가깝다. 저차원에서는 A2와 더 가깝다.

고차원에서의 B와 A1의 중간 지점은 Sparse 한 데이터로 학습이 진행되어 latent space 상에 예측하지 못한 데이터를 포함하고 있을 수 있다.

저차원에서의 B와 A1의 중간 지점은 Dense 한 데이터로 학습이 진행되어 latent space 상에 예측 가능한 데이터를 포함하고 있을 수 있다.
Autoencoder 에서 차원을 줄이면서 Bottleneck hidden layer를 만드는 이유는 입력 데이터를 압축시켜 Latent 정보를 얻기 위함도 있고, 어느 정도 의도한 결과물을 생성해 내는 것에 있다. 여기서 '어느 정도' 라고 한 이유는, input에 대해 output 하나가 아닌 분포를 생성해 내게 되면 좀 더 다양한 결과물을 생성해 낼 수 있기 때문이다. (= VAE)
Autoencoder 실습
https://github.com/oksk1111/ai_test/blob/main/autoencoder(oksk1111).ipynb
주제: Autoencodr를 통해 Fashion MNIST input으로 output 예측하기
(* FashionMNIST는 10개의 의류 class를 구별하기 위한 28x28 흑백 이미지 데이터셋)
해당 예제에선 input 에 해당하는 x의 차원을 784(=28x28)에서 latent space 차원인 64로 축소합니다.
이후 Encoder, Decoder를 Dense 레이어로 정의합니다.
# 모델 정의
class Autoencoder(Model):
def __init__(self, latent_dim, shape):
super(Autoencoder, self).__init__()
self.latent_dim = latent_dim
self.shape = shape
self.encoder = tf.keras.Sequential([ # Encoder 계층
layers.Flatten(),
layers.Dense(latent_dim, activation='relu'),
])
self.decoder = tf.keras.Sequential([ # Decoder 계층
layers.Dense(tf.math.reduce_prod(shape).numpy(), activation='sigmoid'),
layers.Reshape(shape)
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
shape = x_test.shape[1:]
latent_dim = 64 # 차원 축소
autoencoder = Autoencoder(latent_dim, shape)테스트 결과

Autoencoder를 이용한 다양한 변형
1. 이상탐지 (Anomaly Detection)

Autoencoder가 input과 output이 같아지도록 학습을 하게 되고, 해당 주요 특징을 제외한 부분을 noise로 인식하여 loss가 커지게 되고, 해당 loss 가 일정 threshold를 넘으면 비정상으로 판명하는 형태로 이상탐지가 가능하다.
위 그림에선 Normal sample 에 비해 Abnormal sample의 빨간색 부분이 추가되면서 noise에 의한 loss가 발생하여 비정상이라 탐지할 수 있다.
실습
주제: ECG5000 심전도 데이터를 통해 비정상 심전도 파악하기
(* ECG5000 은 각각 140개의 데이터 포인트가 있는 5000개의 심전도가 포함된 데이터. 0은 비정상리듬, 1은 정상리듬)
# 모델 정의
class AnomalyDetector(Model):
def __init__(self):
super(AnomalyDetector, self).__init__()
self.encoder = tf.keras.Sequential([ # Encoder 정의
layers.Dense(32, activation="relu"), # 140 -> 32
layers.Dense(16, activation="relu"),
layers.Dense(8, activation="relu")])
self.decoder = tf.keras.Sequential([ # Decoder 정의
layers.Dense(16, activation="relu"), # 8 -> 16
layers.Dense(32, activation="relu"),
layers.Dense(140, activation="sigmoid")])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = AnomalyDetector()
결과


정상 임계값과 오류 임계값 구분
Accuracy = 0.945 Precision = 0.9922027290448343 Recall = 0.9089285714285714
2. 이미지 노이즈 제거 (Denoising Autoencoder)
Input data에 random noise를 추가하더라도 노이즈가 없는 output data를 얻도록 하는 것이 목적이다.
Manifold 상에서는 똑같지만 원본 데이터와는 다른 노이즈가 추가된 데이터로 Encoder와 Decoder를 학습한다.
노이즈 제거의 방식으로 이미지의 원본을 복구(Image Restoration)하거나 고해상도 변경(Super Resolution)등의 작업도 진행의로의 응용이 가능하다.
(* 참고: PPAPNet - 노이즈를 추가하여 원본 복구가 불가능하게 하는 Autoencoder)
수식
original input: x ∈ ℝ^d
random noise q(x̃|x)
corrupted input x̃ ∈ ℝ^d (해당 input data 를 encoder에 입력)
(* 나머지 수식은 Normal Autoencoder와 동일)
실습
주제: Fashion MNIST 데이터에 임의의 노이즈를 추가한 후 예측하기
이미지에 임의의 노이즈를 준 Input data

# 모델 설계
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2), # 이미지 처리를 위해 Convolution 계층 추가. 일반 리니어 계층으로 하여도 무방
layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3, 3), activation='sigmoid', padding='same')])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
결과

3. Variational Autoencoder
데이터 분포를 이용한 생성형 모델이다.
확률 분포를 이용한 확률적 오토인코더이다. (Probabilistic Autoencoder)
효율적인 근사 베이즈 추론 방법인 Variational Bayesian inference를 수행한다.
주어진 input에 대해 encoder는 평균(=μ)과 표준편차(=σ)를 만들어 정규분포를 만들어 Sampling을 수행한후 data를 넘긴다.
Decoder에서는 해당 sampling data를 통해 train 샘플을 닮은 최종 출력을 만든다.

Loss 계산
Input을 재생산 하기 위한 손실(=Reconstruction Error)과 정규분포를 단순화 하기 위한 정규화(=Regulation) 값을 추가하고 Output 분포와 Input 분포 사이의 차이를 KL Divergence로 구한 값을 추가한다.
실제 Loss minimize 시, Input/Output KLD를 구하기 어려우므로, 분포차이는 0보다 크므로 해당 값을 제외한 채 Reconstruction과 Regulation 값만을 가지고 Loss를 Minimize 하여 Loss를 구한다.

4. Generative Adversarial Networks (GAN)
신경망을 서로 겨루게 하고 경쟁을 통해 신경망 성능을 향상하는 것을 목표로 한다.
Generator
랜덤한 분포(보통 표준정규분포)를 input으로 받고 이와 유사한 output data(=fake data)를 출력
랜덤한 input은 생성할 값의 잠재 표현으로 가정한다.
Generator는 VAE의 Decoder와 같은 기능을 제공한다.
목표는 가짜 output을 진짜 데이터와 유사하게 나오도록 하는 것.
Discriminator: Generator에서 얻은 Fake output과 Train 데이터의 실제 값을 입력으로 받고 진짜인지 가짜인지 판별한다. 목표는 output 구분을 명확히 하는 것.
Loss 계산

G = Generator, D = Discriminator
x = input, z = random noise
1) Discrimanator loss -> max D
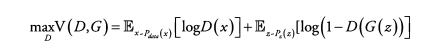
Discriminator의 Objective function을 Loss function 형태로 변경
max_D를 min_D로 바꾸기 위해 Real 데이터가 들어오는 경우의 term에 마이너스를 붙인다.

BCE Loss 형태로 변경하여 계산한다.
2) Generator 입장 -> min G

노이즈 z를 받아서 Fake 데이터를 생성하고, 이것이 Real로 구분되도록 한다.
min_G를 max_G로 바꿔 log(D(G(z))) term을 학습한다.

BCE Loss 형태로 변경하여 계산한다.
5. 기타
DCGAN (Deep Convolutional GAN)
ProGAN
StyleGAN
CycleGAN
StarGAN