|
* 인공지능 모델 구축 과정 1. 가설(Hypothesis; H(x))을 생성 - 수식 2. 훈련데이터로 학습 수행하여 모델 구축 ◾ 손실함수(Cost function)를 통해 가설의 파라미터 조정을 통해 오차를 줄여나감(최적화) -> 모델 완성 (*) 손실함수(Cost function) : 가설의 최적값을 찾기 위한 별도 함수 - 손실함수의 그래프는 Convex 형태여야 한다. (밥그릇 형태) - Convex 그래프에서 미분을 수행하면 기울기가 나오는데, 기울기가 가장 완만한 곳이 가장 손실이 적은 부분! 3. 검증데이터로 #2의 모델 검증 |
선형 회귀 모델
- 선형 방정식으로부터 출력값을 예측하는 모델 (예: y = Wx + b)
(*) 왜 회귀라고 하나?
💡 Tip
- 회귀는 오차(y - ŷ)가 평균으로 회귀하는 것 (y: 실제값, ŷ: 예측값)
- '회귀 모델링은 오차가 평균으로 회귀하도록 만든 모델
1. 가설
◾ (*) x = 입력, 특성(feature); y = 출력, 레이블(label)


2. 최적화
◾ 사용되는 손실함수: MSE (Mean square error; 오차자승의 합의 평균)

(*) 제곱을 쓰는 이유
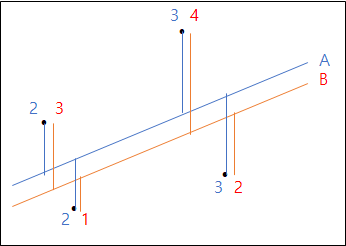
💡 Tip
1) 절대값 오차합
- A 방정식 => 2 + 2 + 3+ 3 = 10
- B 방정식 => 3 + 1 + 4 + 2 = 10
-> 두 방정식간의 오차의 차이점이 없다!
2) 제곱식 오차합
- A 방정식 = 4 + 4 + 9 + 9 = 26
- B 방정식 = 9 + 1 + 16 + 4 = 30
-> 두 방정식간 오차 구분 가능
◾ 그래프 형태: Convex

◾ 오차가 작은 값 찾기
- 기법: 경사하강법 (Gridient descent algorithm)
- 방식
1) 오차함수의 적당한 시점에서 미분 수행 (랜덤위치에서 시작)
2) 기울기가 작은 값이 되는 곳으로 일정범위(learning rate) 이동
3) 기울기가 완만한 곳으로 수렴하는 곳에서 멈춘 후 해당 파라미터 값을 업데이트

- 주의: 경사하강법 적용 전 모든 특성들이 스케일링 되어 있어야 함
3. 성능평가
- MSE는 오차의 크기를 알 수 있지만, 회귀모델의 최종 성능 평가 어려움
- 지표: R-square

4. 구현
- 데이터:

- 모델 구축
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#----- 데이터셋 생성 -------------------------------------
n_samples = 200
x = np.random.randn(n_samples)
# 계수 및 절편
w = 2
b = 3
# 노이즈 추가; np.random.randn(n_samples)
y = w*x + b + np.random.randn(n_samples)
plt.scatter(x,y, s=10)
#----- 선형 모델 생성1: 직접 알고리즘 구현 ----------------
num_epoch = 10 # 학습 수행 횟수
lr = 0.7 # Learning Rate
w = np.random.uniform()
b = np.random.uniform()
for epoch in range(num_epoch):
y_pred = w*x + b
error = np.abs(y_pred - y).mean() # 예측치와 실제값 간의 차이 평균 -> 에러를 줄여야한다
print(f"{epoch:2} w1 = {w:.6f}, b = {b:.6f} , error = {error:.6f}")
w = w - lr*((y_pred - y)* x).mean()
b = b - lr*((y_pred - y)).mean()
#----- 선형 모델 생성2: 라이브러리 이용 ----------------
from sklearn.linear_model import LinearRegression
leg = LinearRegression()
leg.fit(x.reshape(-1,1), y) # ,fit = GradientDescent 알고리즘; reshape()를 통해 2차원 형태로 입력해줘야 한다.(걍 쓰임이 그러함)
print(x.reshape(-1,1))
print(leg.coef_) # weight 값
print(leg.intercept_) # bias 값
leg.predict([[1],[5],[10]]) # y = wx + b 의 결과 (* 코드: https://colab.research.google.com/drive/1QucRW7tXBsyArFWcHJhF5DbgBKbHE_12#scrollTo=FDlT1sbZIZP2 )
'개발' 카테고리의 다른 글
| DevOps란? CI/CD란? (0) | 2021.06.11 |
|---|---|
| 정규표현식 정리 + 사례 연구 (0) | 2020.11.02 |
| Base64 인코딩/디코딩 (0) | 2020.07.29 |
| 인공지능 - 데이터 전처리 (0) | 2020.03.23 |
| 인공지능 - 머신러닝 이론 (0) | 2020.03.20 |


